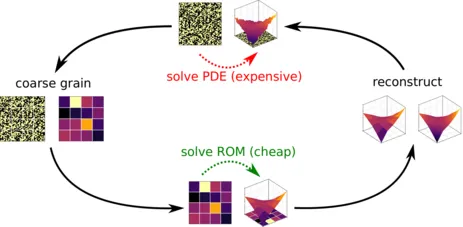
Model-order and dimension reduction of random heterogeneous media

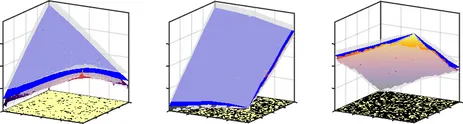
Well-established methods for the solution of stochastic partial differential equations (SPDEs) typically struggle in problems with high-dimensional inputs/outputs. Such difficulties are only amplified in large-scale applications where even a few tens of full-order model runs are impractical. While dimensionality reduction can alleviate some of these issues, it is not known which and how many features of the (high-dimensional) input are actually predictive of the (high-dimensional) output. In this project, we advocate a Bayesian formulation that is capable of performing simultaneous dimension and model-order reduction (Figure 4). It consists of a component that encodes the high-dimensional input into a low-dimensional set of feature functions by employing sparsity-enforcing priors and a decoding component that makes use of the solution of a coarse-grained model in order to reconstruct that of the full-order model. Both components are represented with latent variables in a probabilistic graphical model and are simultaneously trained using Stochastic Variational Inference methods. The model is capable of quantifying the predictive uncertainty due to the information loss that unavoidably takes place in any model-order/dimension reduction as well as the uncertainty arising from finite-sized training datasets. We demonstrate its capabilities in the context of random media where fine-scale fluctuations can give rise to random inputs with tens of thousands of variables. With a few tens of full-order model simulations, the proposed model is capable of identifying salient physical features and produce sharp predictions under different boundary conditions of the full output which itself consists of thousands of components (Figure 5).