Nonlinear Forward and Inverse Stochastic Problems with Applications in Medical Diagnostics
This project is concerned with the numerical solution of high-dimensional, model-based, Bayesian inverse problems. Our motivating application stems from biomechanics where several studies have shown that the identification of material parameters from deformation data can lead to earlier and more accurate diagnosis of various pathologies. We attempt to overcome two of the most important limitations, namely the high-computational cost and the quantification of model errors, by proposing a paradigm shift. Namely, we rephrase the solution of Partial Differential Equations (PDEs) appearing in continuum thermodynamics as a problem of probabilistic inference (probabilistic programming) where unknown state variables are treated as random fields (Figure 1). The solution of the inverse, PDE-constrained problem for solid mechanics problems can be carried out by adjoint-free, second- order methods over the joint space of displacements, stresses and unknown material parameters. The method generalizes to nonlinear problems while the Maximum-A-Posterior estimate recovers the results obtained by the mixed Finite Element method derived from the Hellinger-Reissner variational principle (Figure 2).
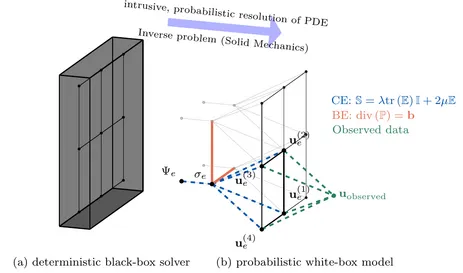
constrained inverse problems by employing probabilistic graphical models where nodes corresponding to element-wise defined quantities are entangled by physical (conservation laws) and phenomenological (constitutive) laws as well as observational data.
