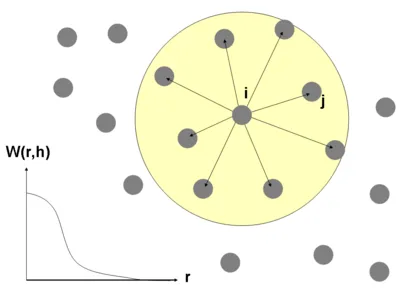
Smoothed particle hydrodynamics (sph)
Smoothed Particle Hydrodynamics (SPH) is a Lagrangian Particle method, where the discretization points are advected in time with the flow field. First introduced independently of Lucy [1] and Gingold and Monaghan [2] in 1977, SPH was originally used to simulate three-dimensional astrophysics problems. This Lagrangian framework enabled the simulation of star formations and interactions of different galaxies where grid-based methods failed mainly due to the problem of large computational domains. Over the years, SPH was applied to a lot of different problems ranging from structural analysis [3] to free-surface flows [4] or even microscopic multi-phase flows [5]. SPH is our method of choice, because it is advantageous especially for multi-phase problems with moving and deforming interfaces. The more, contrary to grid-based methods mass conservation on the interface can be achieved exactly and no interface capturing scheme is needed.
discretization details
Selected Publications
- L. Lucy, A numerical approach to the testing of the fission hypothesis, Astron. J. 82 (1977), 1013.
- R.A. Gingold, J.J. Monaghan, Smoothed particle hydrodynamics: Theory and application to non-spherical stars, Mon. Not. R. Astron. Soc 181 (1977), 375.
- C. Antoci, M. Gallati, S. Sibilla, Numerical simulation of fluid-structure interaction by SPH, Comput. & Structures 85(11-14) (2007) 879-890.
- J.J. Monaghan, Simulating free surface flows with SPH, J. Comput. Phys. 110 (1994) 399-399.
- X.Y. Hu, N.A. Adams, A multi-phase SPH method for macroscopic and mesoscopic flows, J. Comput. Phys. 213(2) (2006) 844-861.