Physics-constrained, data-driven discovery of coarse-grained dynamics
This project is concerned with the discovery of data-driven, dynamic, stochastic coarse-grained models from fine-scale simulations with a view of advancing multiscale modeling. Many problems in science and engineering are modeled by high-dimensional systems of deterministic or stochastic, (non)linear, microscopic evolution laws (e.g ODEs). Their solution is generally dominated by the smaller time scales involved even though the outputs of interest might pertain to time scales that are greater by several orders of magnitude. The combination of high-dimensionality and disparity of time scales has motivated the development of coarse-grained (CG) formulations. These aim at constructing a much lower-dimensional model that is practical to integrate in time and can adequately predict the outputs of interest over the time scales of interest. The challenge in multiscale physical systems such as those encountered in non-equilibrium statistical mechanics, is even greater as apart from the identification of an effective model, it is crucial to discover simultaneously, a good set of CG state variables. In this project, we treat the CG model as a probabilistic state-space model where the transition law dictates the evolution of the CG state variables and the emission law the coarse- to-fine map (Figure 6). Naturally, one of the most critical questions pertains to the form of the CG evolution law which poses a formidable model selection issue. Correct identification of the right-hand side terms involved can also reveal qualitative features of the coarse-scale evolution such as the type of constitutive relations. In order to avoid overfitting as well as endow the estimates with robustness even in the presence of limited data, we invoke the principle of parsimony that is reflected in the sparsity of the solutions.
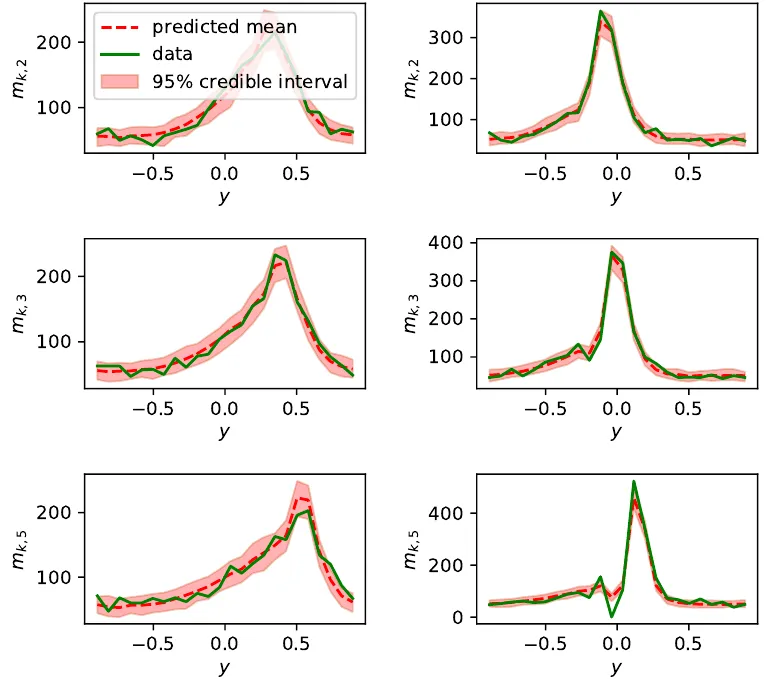
Burgers’ equation. The left and the right columns correspond to two different initial conditions
and the rows represent snapshots of the system at different time instances. The green dashed line
represents the true time evolution of the system. The red shaded area is the predicted 95%
credible interval and the red dashed line the predicted mean.