Fluid-Structure Interaction: Formulations
Christoph Ager, Matthias Mayr, Benedikt Schott
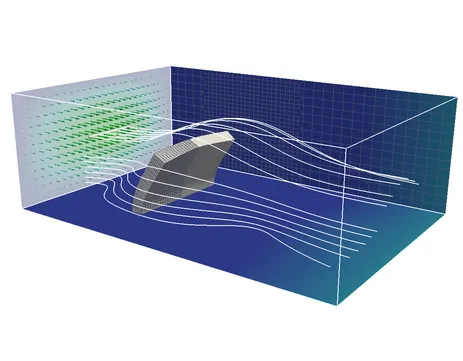
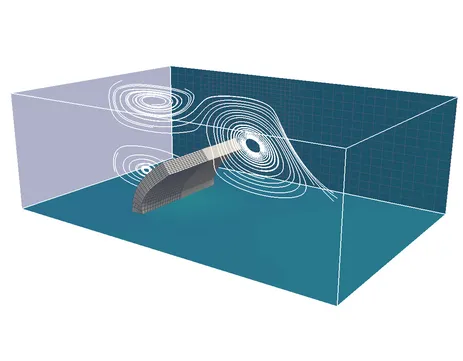
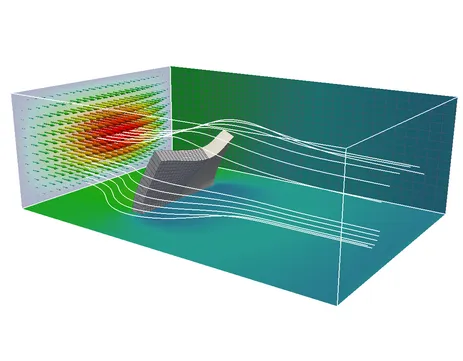
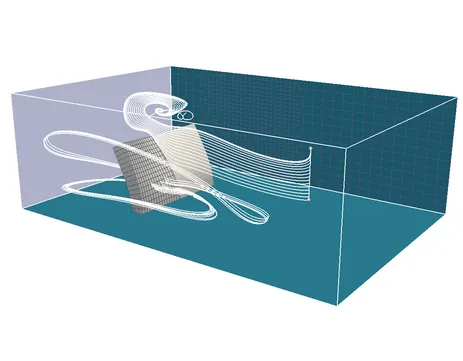
FSI approaches can be distinguished by their different formulations needed to describe the material motion in each participating field. Most research and commercial FSI-codes are based on the Arbitrary Lagrangian Eulerian (ALE) method and node-matching meshes. The essential feature of the ALE based methods is that the fluid field is formulated and solved on a deforming grid. Within the last years, our research group contributed a number of different FSI schemes and has applied them to a variety of problems.
For many reasons the creation of matching fluid and structure meshes at the interface can be cumbersome or even impossible. We have therefore developed an extension of the classical ALE approach to non-conforming grids with the help of the dual mortar method. This method handles the additional complexity at negligible computational cost and does not introduce any restriction on the particular choice of finite element formulations for the single fields.
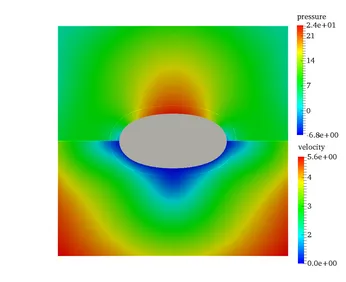
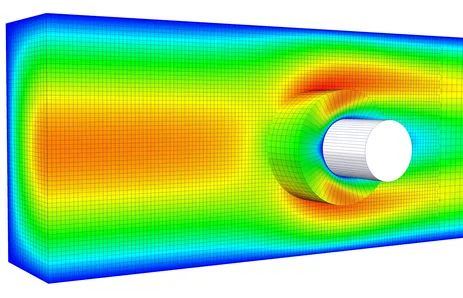
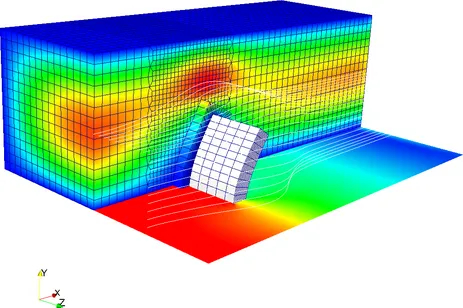
Fixed-grid methods represent a promising approach when dealing with FSI involving large deformations of the structure. Even the most advanced ALE based schemes come to their limits where only re-meshing helps to prevent severe fluid mesh distortion. In fixed-grid methods, the entire fluid domain is described by an Eulerian fluid formulation without the need for any moving or deforming fluid meshes. The structural body is still described in a classical Lagrangean frame of reference and its mesh is embedded into the fluid grid in a geometrically unfitted fashion. The fluid-structure interface divides the fluid domain into a physical and a ghost domain. To describe this discontinuity in the fluid field the Cut Finite Element Method (CutFEM) is used. Since the interface is not aligned with element edges, weak constraint enforcement techniques are necessary to apply interface conditions. We developed a Nitsche-type method which allows to provide stable and optimal convergent coupling schemes independent of the location of the structural mesh within the fluid for low- and high-Reynolds-number flows. Thereby, no new variables are introduced into the system. The independent treatment of the fluid and the structural mesh provides highest flexibility with regards to motions, rotations and deformations of the structure within the surrounding fluid such that even contact of immersed bodies (FSCI) can be simulated. Moreover, meshing becomes as simple as possible and regular remeshing can be avoided.
An important prerequisite for achieving reliable results for complex FSI problems is a proper resolution of flow features around the structural surface, where boundary layers, flow separation and re-attachment can occur. Thus, we are working on a hybrid approach combining the advantages of fixed-grid and ALE techniques. The fundamental idea is to add a deformable fluid patch around the structure surface, which fits the structural mesh at the common interface and is embedded into a fixed or independently moving background fluid mesh in an unfitted way using the CutFEM. For coupling the non-fitting flow approximations, a stabilized Nitsche-type domain decomposition method has been developed. Using ALE techniques allows the embedded fluid patch to follow the structure in its motion. This still allows for large deformations and rotations of flexible bodies in the surrounding fluid and further guarantees sufficient resolution of the flow features in the vicinity of the structure all the time.