Increasing efficiency of mechatronic devices is often achieved through lightweight design using flexible mechanical structures like beams, strings, plates, and so on. This leads to a more complex modeling procedure often relying on the theory of nonlinear continuum mechanics. Due to the limited number of actuators the considered systems are highly under-actuated, which makes their analysis and control design challenging. In this project, we focus on efficient modelling and control methods to overcome the problems associated with this system class.
Energy-Based Formulations of Nonlinear Elastodynamics
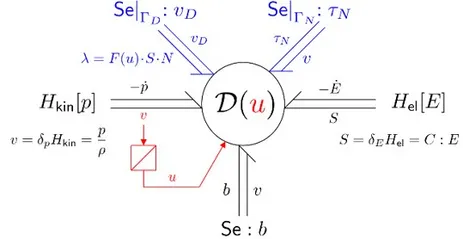
Port- and energy-based formulations are favorable for modular and structured modeling of large-scale interconnected and coupled multi-physics phenomena. The port-Hamiltonian (PH) approach emphasizes the interconnection or energy exchange mechanisms and the interactions of subsystems through their (boundary) ports, i.e., interfaces of dual power variables. Numerical methods that conserve important geometric properties are well-known in their corresponding engineering disciplines, e.g., mixed finite elements for velocity-stress formulations of nonlinear elastodynamics. For example, we considered hyperelastic strings, and the general setting of geometrically nonlinear continua from the perspective of boundary control systems, their structure-preserving discretization in space and time, retaining the underlying PH structure.