Model Reduction of Nonlinear Systems

Nonlinear model reduction has gained a lot of attention in the last past 10 years. Mainly because a lot of technically relevant and real-life systems (e.g. in automotive, aeronautic, electromechanical and circuit applications) can be modelled by large-scale systems of differential equations, where often nonlinearities arise. The challenges are hereby twofold: the high number of degrees of freedom and the nonlinear nature of the underlying equations.

Fully nonlinear model order reduction

The aim of nonlinear model order reduction is to approximate the original nonlinear model with a reduced-order model that does not only involve much less state variables, but also which guarantees computational savings when integrating its differential equation. The main tasks are therefore:

1. The efficient computation of a reduced basis that comprises the most dominant nonlinear dynamics for the projection-based reduction of degrees of freedom
2. The application of so-called hyperreduction methods for the effective evaluation of the nonlinear terms

Most of the existing nonlinear reduction approaches (e.g. the Proper Orthogonal Decomposition (POD) or the Trajectory Piecewise Linear Approximation (TPWL)) rely on expensive training simulations of the original model to compute the reduced basis. In our group, however, we also actively work on simulation-free nonlinear model reduction methods, where the computed reduced basis is independent of the control input. Towards this aim, we try to extend well-known linear reduction methods, like balanced truncation and Krylov subspace methods, to the fully nonlinear setting.

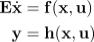
At MORLab we theoretically investigate simulation-free approaches, but also develop numerically efficient nonlinear model reduction algorithms and benchmark models in MATLAB.

Weakly nonlinear model order reduction

At MORLab we also investigate model order reduction for special classes of nonlinear systems. More specifically, we focus on weakly nonlinear systems such as:

These system classes represent an interface between fully nonlinear and linear dynamic systems and are, due to the structure, closely related to linear state-space systems. Therefore, many well-known system-theoretic (e.g. transfer functions, Gramians, H2-norm, etc.) and model reduction concepts (e.g. balanced truncation, Krylov subspaces) can be generalized to the bilinear and quadratic-bilinear setting.

In our group, we actively research on the system theory and model order reduction methods for these special nonlinear system classes. Ongoing work mainly concentrates on

• MIMO bilinear and quadratic-bilinear systems
• Extension of Krylov subspace methods and H2-optimal approaches
• Stability preservation

At MORLab we theoretically investigate all these topics, but also develop numerically efficient model reduction algorithms and benchmark models in MATLAB.

Related References

Cruz Varona, M.: On the H2-pseudo-optimal bilinear model reduction. Applied Numerical Analysis Seminar, Virginia Tech, Blacksburg (VA), USA, 2017

Cruz Varona, M.: Two-sided Moment Matching-Based Reduction for MIMO Quadratic-Bilinear Systems. 11. Elgersburg Workshop, Elgersburg, 2017

Cruz Varona, M.; Fiordelisio Junior, E.; Lohmann, B.: Krylov subspace methods for model reduction of MIMO quadratic-bilinear systems. 3rd Workshop on Model Reduction of Complex Dynamical Systems (MODRED), Odense, Denmark, 2017

Cruz Varona, M.; Lohmann, B.: Simulation-free nonlinear model order reduction by (imitated) Moment Matching. 12. Regelungstechnischer Workshop Schloss Hirschberg, 2016

Cruz Varona, M.; Olcay, E.; Lohmann, B.: Interpolation-based H2-pseudo-optimal model reduction of bilinear systems. GMA Fachauschuss 1.30 "Modellbildung, Identifikation und Simulation in der Automatisierungstechnik", Anif, Austria, 2016

Cruz Varona, M.: Krylov subspace model reduction for bilinear and MIMO quadratic-bilinear systems. Workshop on Model Order Reduction and Optimization, Opatija, 2016

Cruz Varona, M.: A smooth transition: from moving loads to bilinear model reduction. Augsburg-München Workshop on Model Reduction, 2016

Cruz Varona, M.: Interpolation-based model reduction of nonlinear systems. CSC Seminar, Max-Planck-Institut für Dynamik komplexer technischer Systeme, Magdeburg, Germany, 2016

Buttelmann, M.; Lohmann, B.: Optimierung mit Genetischen Algorithmen und eine Anwendung zur Modellreduktion, Automatisierungstechnik (at) 52 (2004), Heft 4, pp. 151-163

Yousefi, A.; Lohmann, B.; Buttelmann, M.: Row by Row Structure Simplification, Proceeding of the 2004 American Control Conference, Boston, Massachusetts, 2004.

Salimbahrami, B.; Lienemann, J.; Lohmann, B.; Korvink, J. G.: A Simulation Free Reduction Scheme and Nonlinear Modelling of an Electrostatic Beam, 10th IFAC/IFORS/IMACS/IFIP Symposium on Large Scale Systems: Theory and Applications, Osaka 2004

Linemann, J.; Yousefi, A.; Korvink J.; Lohmann, B.: Nonlinear heat transfer modelling and reduction, IEEE Mediterranean Conference on Control and Automation, 2004.

Salimbahrami, B.; Lohmann, B.: A Simulation Free Nonlinear Model Order Reduction Approach and Comparison Study, Mathematical and Computer Modelling of Dynamical Systems (MCMDS), Vol. 10, Numbers 3-4, September-December 2004, pp. 317-329.

Salimbahrami, B.; Lohmann, B.: A Simulation Free Nonlinear Model Order Reduction Approach and Comparison Study, Proceedings of the 4th  MATHMOD, Vienna 2003, pp. 429-435.

Buttelmann, M.; Lohmann, B.: Two Optimization Methods for Solving the Problem of Structure Simplification of Non-Linear Systems, Proc. of IEEE internat. Conference on Methods and Models in Automation and Robotics, Szczecin, Poland, 2002, pp. 1257-1262.

Buttelmann, M.; Lohmann, B.: Non-linear model reduction by genetic algorithms using a system structure related fitness function. Proceedings of the European Control Conference (ECC) 2001, Porto, Portugal, pp. 1870-1875.

Lohmann, B.: Application of Model Order Reduction to a Hydropneumatic Vehicle Suspension, IEEE Trans. Control Sys. Tech., Vol.3, (1995) pp.102-109.

Lohmann, B.: Ordnungsreduktion und Dominanzanalyse nichtlinearer Systeme, Automatisierungstechnik 42 (1994), pp. 466-474.