Nichtlineare Strukturmechanik

Inhalt

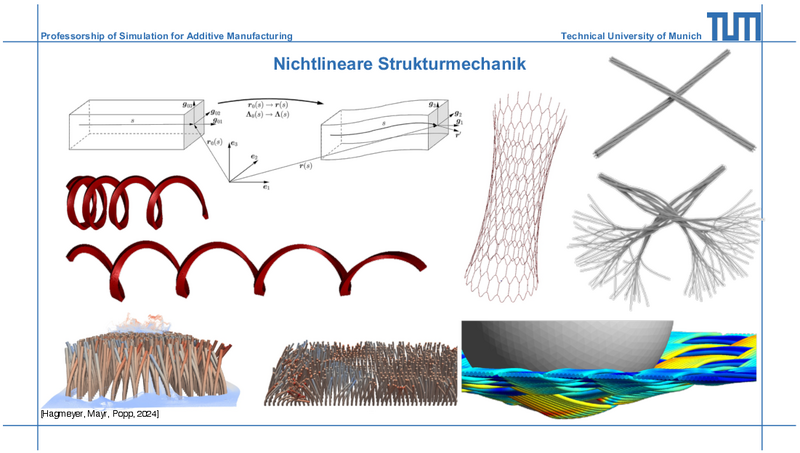
Der Fokus der Vorlesung liegt auf geometrisch nichtlinearen Balkentheorien als Beispiel für nichtlineare Modelle der Strukturmechanik. Schlanke balken- oder faserartige Komponenten sind essentielle Bestandteile mechanischer Systeme in zahllosen Anwendungsfeldern und wissenschaftlichen Disziplinen. Beispiele sind hochfeste Seile und Gewebe, faserverstärkte Verbundwerkstoffe oder synthetische Polymerwerkstoffe. Auf gänzlich anderen Zeit- und Längenskalen sind solche Komponenten etwa relevant zur Analyse des Supercoiling-Prozesses von DNA-Strängen, der Eigenschaften von Carbon Nanotubes oder des Cytoskeletts biologischer Zellen. Letzteres stellt ein biopolymeres Netzwerk aus schlanken Filamenten dar, welches die Mechanik von Zellen entscheidend beeinflusst. Oftmals können diese schlanken Komponenten mittels geometrisch nichtlinearen Balkenmodellen beschrieben werden.

Im Rahmen der Vorlesung wird insbesondere die sogenannte geometrisch exakte Balkentheorie betrachtet, welche basierend auf einer fundamentalen kinematischen Annahme sowohl große Rotationen als auch große Dehnungen konsistent, d.h. ohne weitere Approximationen, abbilden kann. Insbesondere werden in diesem Zusammenhang die geometrisch exakte Simo-Reissner Balkentheorie (kinematische Annahme: Balkenquerschnitte bleiben eben; nichtlineares Gegenstück zur linearen Timoshenko Balkentheorie) sowie die geometrisch exakte Kirchhoff-Love Balkentheorie (kinematische Annahme: Balkenquerschnitte bleiben eben und senkrecht zur Mittellinie; nichtlineares Gegenstück zur linearen Euler-Bernoulli Balkentheorie) sowie deren Interpretation als ein 1D Cosserat-Kontinuum, d.h. eine Kontinuumstheorie mit je drei translatorischen und drei rotatorischen Freiheitgraden, eingeführt.

Da das Vorhandensein großer Rotationen ein entscheidendes Merkmal vollständig nichtlinearer Strukturtheorien ist, wird eingangs die Theorie großer Rotationen (insbesondere die Theorie der speziellen orthogonalen Gruppe SO(3)) eingeführt. Basierend auf diesen Grundlagen, wird anschließend die geometrisch exakte Balkentheorie als eine nichtlineare Cosserat-Kontinuumstheorie bestehend aus (jeweils translatorischen und rotatorischen) Verzerrungsmaßen, Spannungsresultierenden, Konstitutivbeziehungen und mechanischen Gleichgewichtsbedingungen (jeweils in räumlicher oder materialer Form) postuliert. Darüber hinaus wird gezeigt, wie die geometrisch exakte Balkentheorie aus den Gleichungen der nichtlinearen Kontinuumsmechanik unter Einbeziehung der fundamentalen kinematischen Annahme abgeleitet werden kann. Zu diesem Zweck wird auch eine Kurzzusammenfassung der nichtlinearen Kontinuumsmechanik von Festkörpern (3D Boltzmann-Kontinuum) präsentiert, welche u.a. auch die strukturellen Ähnlichkeiten zur geometrisch nichtlinearen Balkentheorie (1D Cosserat-Kontinuum) veranschaulicht.

Abschließend gibt die Vorlesung einen Ausblick auf numerische Diskretisierungs- und Lösungsverfahren (insbesondere Diskretisierung mittels der Finite Elemente Methode) sowie alternative Modelle der nichtlinearen Strukturmechanik (z.B. alternative bzw. reduzierte nichtlineare Balkentheorien oder nichtlineare Theorien für Schalen und Platten).