Advanced Instability Analysis
by R. Blumenthal, S. Bomberg, T. Stanko and Wolfgang Polifke
Background and Motivation
Thermoacoustic instabilities, i.e. self-excited oscillations, are a major concern in combustion systems, such as gas turbines or rocket engines: pressure and temperature peaks may lead to fatigue and failure of the involved materials. Also, the combustion process may be shifted to an off-design point so that higher emissions occur. It is, therefore, of great importance to study system behavior at an early stage in the design process.
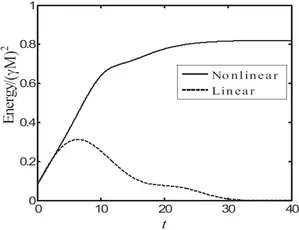
Commonly, the equations governing the system dynamics are linearized and transformed into frequency domain or into a state-space formulation. Analysis of the eigenvalues of the underlying system operator then allows to draw conclusions on the system's asymptotic state, i.e. its long-term behavior. However, it was shown that operators describing the dynamics of thermoacoustic systems generally are non-normal, i.e. their eigenvectors/eigenfunctions are not orthogonal [2]. As a consequence, certain effects are present in such systems that cannot be captured by means of the classical stability analysis. Due to the non-normality, the amount of fluctuation energy can temporarily increase, even for a linear, asymptotically stable case. It is argued that this transient growth can lead to fluctuation amplitudes large enough to no longer allow for the assumption of linearity [3,4]. In that case, nonlinear effects must be taken into account which may take the system to a different asymptotic state: Figure 1 shows the development of fluctuation energy in a thermoacoustic system over time. For the linear case, after an initial transient growth, all oscillations decay. If nonlinearities are accounted for, the system goes into a limit cycle. Here, one speaks of transient growth triggering instability. In general, the strength of transient growth, and whether it occurs at all, is heavily depending on the initial conditions. Another related question is the definition of (a norm of) fluctuation energy.
Nonlinear systems behave very differently compared to linear systems. One way to characterize them is by analyzing so-called bifurcation diagrams. Bifurcation diagrams show the system behavior as an answer to the variation of a certain parameter (e.g. power output). At the bifurcation points the system behavior changes qualitatively. Most commonly, in the framework of thermoacoustics, a steady state and a stable limit cycle can be observed. Furthermore, chaotic behavior is possible as well. Often, there exist hysteresis effects. System stability can then be determined for a range of operating conditions and regions of stability, bi-stability and instability can be identified. Figure 2 depicts a bifurcation diagram of the amplitude of velocity fluctuations as it may be obtained e.g. for a Rijke Tube with its length as bifurcation parameter [2].
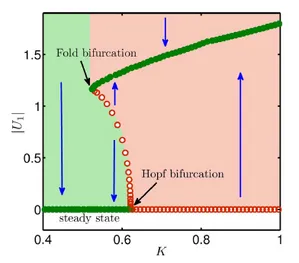
The knowledge about the nonlinear system dynamics gained by means of bifurcation analysis helps to develop appropriate reduced models and identification schemes.
Project Goals: Pertinent Questions
As pointed out in the preceding section, the effects of nonlinearity and non-normality in thermoacoustic systems may render the classical stability analysis inadequate. Thus, a machinery for an advanced instability analysis is required. In order to derive and develop such a set of tools, a number of topics shall be studied:
- Under which circumstances does non-normality trigger the system into a nonlinear instability regime?
- Does there exist a universality of transition mechanisms?
- Which initial conditions lead to maximum growth (optimal condition)? Are these initial conditions physically attainable?
- By which means does inter-modal energy transfer occur?
- Which model structures and identification schemes are suitable for describing such systems?
Project Summary
The effects of non-normality (in combination with nonlinearity) on thermoacoustic systems shall be studied for the case of laminar premix flames. Two flame shapes shall be investigated: a conical flame and a V-shaped flame. Numerical simulations are expected to yield information about appropriate identification schemes and model structures for reduced models. Consequently, tools shall be developed that allow to perform an advanced stability analysis for systems of an applied interest with a reasonable amount of computational effort and time.
The project is subdivided into different work packages; each one allowing to follow a different approach, in order to tend finding answers to the above mentioned project goals. The corresponding flow chart is shown in Fig. 3.
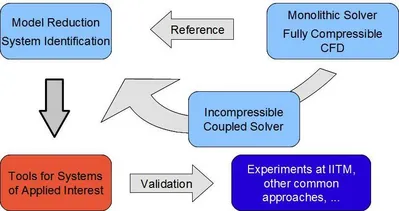
A so-called monolithic numerical solver is to be implemented. The fully compressible Navier-Stokes Equations are solved including flow-combustion-acoustics coupling. This solver is intended to generate reliable reference data as well as to study the impact of various parameters on non-normality and the related system identifiability.
In a second approach, a less computationally involving solver is to be created. Assuming low Mach number and compact flames, asymptotic analysis allows to divide the numerical domain into an incompressible hydrodynamic region and an acoustic region [1]. Different models, discretization and solution techniques may be applied to the two regions. This procedure is expected to drastically reduce the computational effort, so that this solver may serve as a starting point for the analysis of systems of applied interest. It should be mentioned that the impact of certain terms coupling hydrodynamics and acoustics is currently a matter of debate.
The third approach consists of finding reduced-order models, which are capable of describing thermoacoustic systems and also of capturing the dominant non-normal and nonlinear effects. The aim is to reduce computational costs by identifying the dominant structures at play. This is to be done by linear as well as nonlinear System Identification Techniques (SI) and also by techniques reducing the size of the system, such as Global Modes analysis. The initial conditions leading to maximum growth shall be found by Singular Value Decomposition for linear systems and Adjoint Looping for more complex and nonlinear systems. Thereby it is important to find out the dominant quantities which should be included in the definition of a system norm, in order to achieve an accurate measure to identify and to describe the thermoacoustic system.
The numerical studies shall be complemented by – and validated against – experimental data obtained at the Indian Institute of Technology in Madras, India. Furthermore, a comparison to results from other existing methods (e.g. Flame Describing Function technique) shall be carried out.
Acknowlegment
With the support of the Technische Universität München - Institute for Advanced Study, funded by the German Excellence Initiative.
Selected References
[1] Balaji, C. and Chakravarthy, S.R. A Simultaneous Multiple Space-/Time-Scale Formulation of Fluid Flow Problems with Application to Combustion Thermoacoustics. In n3l – Int'l Summer School and Workshop on Non-Normal and Nonlinear Effects in Aero- and Thermoacoustics, TU München, Munich, Germany, 2010.
[2] Balasubramanian, K. and Sujith, R.I. Thermoacoustic Instability in a Rijke Tube: Non-normality and Nonlinearity. Physics of Fluids, 20, 044103, 2008.
[3] Juniper, M.P. Triggering in the Horizontal Rijke Tube: Non-normality, Transient Growth and Bypass Transition. J. Fluid Mech., 667:272—308, 2011.
[4] Schmid, P.J. Nonmodal Stability Theory. Annu. Rev. Fluid Mech., 39:129—62, 2007.
[5] Subramanian, P., Mariappan, S., Sujith, R.I. and Wahi, P. Application of Numerical Continuation to Bifurcation Analysis of Rijke Tube. In n3l – Int'l Summer School and Workshop on Non-Normal and Nonlinear Effects in Aero- and Thermoacoustics, TU München, Munich, Germany, 2010.