Dynamics of Skin Friction and Heat Transfer of a Cylinder in Pulsating Cross Flow

Dipl.-Ing. Armin Witte, Prof. Wolfgang Polifke PhD (CCNY)

Motivation

The drag and heat transfer of a cylinder in cross flow is one of the archetypal problems in thermo-fluid mechanics. The majority of studies addresses these quantities under steady-state flow conditions. However, the unsteady case is also of relevance e. g. for applications like hot-wire anemometry or the Rijke tube. In the latter case, a heated wire mesh in pulsating cross flow can drive a thermoacoustic instability. Stability limits and pulsation amplitudes depend on the response of heat transfer to velocity fluctuations.

Figure 1: Instantaneous temperature field of a hot cylinder in cold cross-flow (CFD).

State of the art

Lighthill [1] studied the response of skin friction and heat transfer to small-amplitude fluctuations in the free stream velocity u_∞. Using the boundary layer equations and a perturbation ansatz he was able to derive approximate expressions for low and high frequencies valid for mean flow Reynolds number s Re>10. One major finding was the time constant for a first order approximation of the heat transfer frequency response which was determined to τ=0.2 d/u_0,∞ with the cylinder diameter d and the unperturbed mean flow velocity u_0,∞.

In a study by Gersten [2] these results were refined with respect to the transition between low and high frequencies. He also considered specifically two types of boundary layers: stagnation point flow and flat plate flow.

Using the Oseen equations, Bayly [3] was able to find an expression for the frequency response at low Peclét numbers. This approach does not rely on the existence of a certain type of boundary layer but is for usual Prandtl numbers restricted to Re→0.

Upon these analytical studies a number of numerical investigations were carried out, e.g. by Telionis and Romaniuk [4] who solved the boundary layer equations numerically. Kwon and Lee [5] tackled this problem solving linearized Navier Stokes equations incorporating a unique non-dimensionalization. Föller et al. [6] were the first to use system identification techniques together with CFD simulation in this scope.

Method

Figure 3: Schematics of the Output Error model

The core if this project is to study the dynamic responses of skin friction and heat release by the use of the CFD/SI approach which is schematically depicted in figure 2.

CFD simulations of the problem at hand are used to generate time series data. The inlet velocity is created as the superposition of a fixed mean value and a fluctuation in time. This fluctuation is specifically designed to have high power spectral density over the range of frequencies that are of interest. Navier-Stokes equations and a scalar transport equation for the temperature are solved by a Merged PISO/SIMPLE algorithm implemented in the OpenFOAM framework (version 2.3.0). Time series data are acquired at a plane upstream of the cylinder for the velocity (signal) at the cylinder for Nußelt number and friction coefficient (responses).

The acquired time series are used in the system identification procedure. System identification is used to develop a mathematical description, i.e. a model, for a process or system. More specifically a transfer function is built from a given input to a system and its response, which is measured. System identification is widely used in the fields of electrical engineering, economy and psychology and several textbooks deal with different aspects of this methods The CFD/SI method, combining numerical simulation with system identification was proposed by Polifke et al.

For the identification of transfer functions using data from CFD simulations, the chosen model structure is an output error (OE) as depicted in figure 3. The coefficients of the polynomials B and F are found during identification solving a nonlinear minimization problem. The transfer function can easily be converted into an expression for the frequency response or from discrete time to continuous time representation.

Results

Figure 4: Amplitude of skin friction frequency response.

Figure 5: Phase of skin friction frequency response.

Figure 6: Amplitude of heat transfer frequency response.

Figure 7: Phase of heat transfer frequency response.

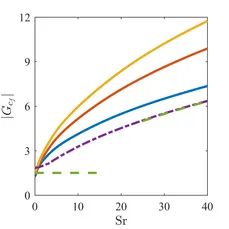
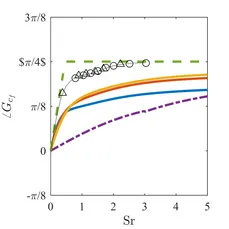
Figures 4 and 5 show amplitude and phase of the skin friction frequency response to velocity perturbations, respectively. Analytical approximations by Lighthill [1] for flat plate flow are shown as dashed lines and dash-dotted lines denote the results from Gersten [2] for stagnation point flow. The frequency response evaluated in this this study is shown as solid lines for three different mean flow Reynolds numbers. Blue denotes the response at Re=0.4 and red and yellow the responses at Re=4 and 40, respectively.

Lighthill and Gersten are not able to predict any dependence on Reynolds number, but it become clear from the figures that it has a huge influence on the amplitude of the skin friction response. The phase exhibits a high frequency limit of +ϖ/4 for all cases. However, the initial rise (the "anticipation time") is different. Compared to the CFD/SI results the anticipation time for stagnation point flow is smaller (smaller slope) and higher for flat plate flow.

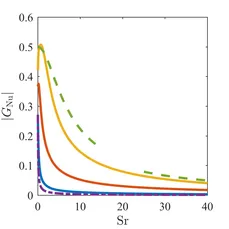
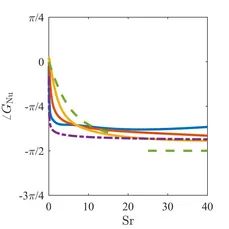
Amplitude and phase of heat release frequency responses are depicted in figures 6 and 7, respectively. The same color coding is used as for skin friction, only Bayly's [3] results are shown as dash-dotted lines instead of Gersten's.

A clear dependence on mean flow Reynolds number is visible here, similar to the response of the skin friction. Lighthill's approximations are again not able to show this. In Bayly's results a dependence on Reynolds number is included. However, values become unphysical if Re>0.5 are considered. The peak gain close to Sr≈1 that was reported by Föller et al. [6] could be confirmed. Moreover, discrepancies in the high frequency limit of the phase can now be attributed to the behavior of the heat release near the rear stagnation point of the cylinder.

References

[1] M. J. Lighthill, The response of laminar skin friction and heat transferto ﬂuctuations in the stream velocity, Proceedings of the Royal Society ofLondon A 224 (1954) 1–23.

[2] K. Gersten, Heat Transfer in Laminar Boundary Layers with Oscillating Outer Flow, no. 97 in AGARDograph, 1965, pp. 423–475.

[3] B. J. Bayly, Heat transfer from a cylinder in a time-dependent cross ﬂow at low Peclét number, Physics of Fluids 28 (12) (1985) 3451. doi:10.1063/1.865298.

[4] D. P. Telionis, M. S. Romaniuk, Velocity and Temperature Streaming in Oscillating Boundary Layers, AIAA Journal 16 (5) (1978) 488–495. doi:1065 10.2514/3.60916.

[5] Y.-P. Kwon, B.-H. Lee, Stability of the Rijke Tube Thermoacoustic Oscillation, J. Acoust. Soc. Am. 78 (78) (1985) 1414–1420.

[6] S. Föller, F. Selimefendigil, W. Polifke, Linear Identification of the Unsteady Heat Transfer of a Cylinder in Pulsating Crossflow, in: Int. Conf.on Jets, Wakes and Separated Flows, Technical University Berlin, Berlin,1075 Germany, 2008.

Acknowledgement

Financial support has been provided by the German Research Foundation (DFG), project PO 710/15-1, whose support is gratefully acknowledged.