Skip to content
Technical University of Munich

Modelling and Validation of joint presumed discrete distributions for LES of turbulent reacting flows

by Frank Fischer and Wolfgang Polifke

Motivation

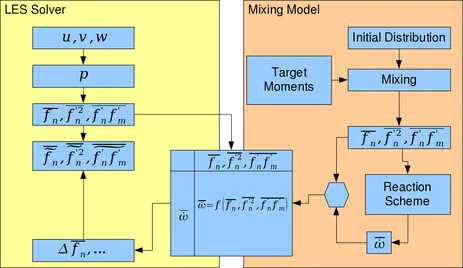
Mixing processes and chemical reactions in turbulent flows play a major role in many technical applications like gas turbines or chemical engineering. The objective of this project is to develop a computational model for subgrid scale mixing of multiple streams (called ”ternary mixing” for three streams) that includes the correlation between the mixture fractions. This model is then used to compute mean reaction rates in LES, while keeping computational efforts minimal when compared to transported PDF methods. In order to futher reduce the computational requirements, possible mixture fraction distributions are to be computed as ensembles of discrete, massless particles in a pre-processing step, stored in a table and then be referred to during the CFD simulation as shown in Figure I.

Figure 1: Basic workflow of the presented model

Theory

In the presented model, distributions are characterized by statistical moments of first (mean values) and second (variances and correlations) order. These moments are transported in the LES as nonconserved passive scalars using appropriate models for the production and dissipation of subgrid scalar variance:

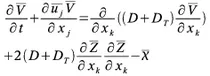
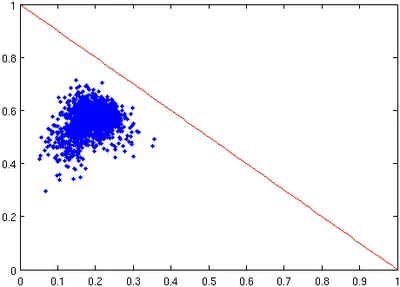
Here, V represents the variance, Z the mixture fraction, and  the scalar dissipation rate which itself is considered to be proportional to the mixing time as presented in [1]. The distribution with the given stochastic parameters can be generated using typical mixing model like IEM, Modified Curl, EMST, or PSP [2]. A sample distribution generated using the Modified Curl Model is shown below.

Figure 2: Example distibution for an altered modified Curl model. Mean values are 0.19 and 0.56 respectively, Variances 0.002 and 0.003. The distribution possesses a correlation of 0.29

Validation

Direct Numerical Simulations have been conducted to generate a database of simple flows incorporating ternary mixing processes. The DNS data is conditionally filtered so that statistical distributions of mixture fractions can be obtained, the filter conditions are adapted to the parameters that the model requires. The distributions can then be compared to the ones generated by mixing models to assess the suitability of the mixing model in question. A DNS-generated distribution is shown in Figure III, it has the same statistical moments as the distribution in Figure II. Futher validation of the model is planned using PIV/LIF experiments for high-Reynolds-number flows where DNS become unsuitable.

Figure 3: Example distibution extraced from DNS. Mean values are 0.19 and 0.56 respectively, Variances 0.002 and 0.003. The distribution possesses a correlation of 0.29

Outlook

In order to complete the model, several issues remain to be solved: In order to perform simulations, a transport equation for the correlation (or covariance) needs to be defined, along with a model for the scalar cross-dissipation, including its production and dissipation. Futhermore it is planned to enable reactive flows in the LES/DNS solver so that the quality of the mixing model can be assessed with regard to the reaction rates obtained by the simulation. Futhermore it is required to implement an efficient algorithm to store and retrieve data from a multidimensional table (5 to 8 dimensions are likely to be needed) in order to keep both computational requirement and memory usage at bay.

References

[1] Subgrid scale variance and disssipation of a scalar field in large eddy wsimulations, Jiménez et al, Physics of Fluids, Vol. 13,. No. 6 (2001), 1748-1754

[2] A mixing model for turbulent flows based on parameterized scalar profiles, W. Meyer and P. Jenny, Physics of Fluids, Volk. 18, 2006.

To top