Multi-scale Modelling of the Population Dynamics of Hydrometeors with Methods of Moments
by Gary Jasor and Wolfgang Polifke
Motivation
This project deals with the modelling of population dynamics of hydrometeors. The goal is to develop a method to describe the time and space evolution of particles populations (e.g. drop population), which is so efficient that it can be applied to weather forecast models. In particular, methods of moments well known in fluid dynamics are used, as they present a great development potential in the fields of cloud physics. These methods of moments (MoM) present the advantage that, while they enable one to describe the effects of microscale processes on the evolution of the moments, knowledge about the macroscopic moments of the size distribution offers feedback on the microstate of a drop population.
Background and method description
One of the main points in the description of fluid systems with a dispersed phase is to know how the particle population evolves in time and space. Elementary physical processes which influence the microscale (order of micrometers to centimetres), like particle growth, collisions of particles leading to coagulation or break-up processes as well as particle births, have to be taken into consideration. Those processes are themselves influenced by the dispersant (that is to say the fluid) : particles are transported by the flow and at the same time, may also be influenced by external forces, such as the gravitational one (sedimentation).
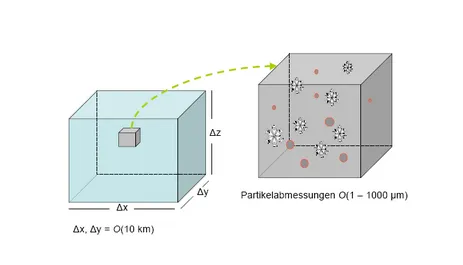
The fluid systems usually have macroscopic dimensions (from couple of meters in technical field to several kilometres in meteorological field). The interest is not put in the microscale processes themselves but merely in describing their effects on the macroscale as exactly as possible.
A special field of application with the mentioned processes is cloud and rainfall physics, which plays an important role in any weather forecast model trying to describe accurately the hydrological cycle. In our case, we focus on water clouds, so that the microprocesses are coagulation, break-up, condensation/evaporation, nucleation and sedimentation (rainfall in gravitational field), while the flow fluid is the air present in clouds, which is a mixture of dry air, steam and water drops with different sizes. In practice the microscale processes which macroscopically influence the clouds and rainfalls, shall be parametrized and expressed thanks to macroscopic variables in order to minimize the computational costs.
In the so-called clouds models in meteorology, the microprocesses leading to a time and space evolution of the raindrops size distribution are ceteris paribus described by the same equations as the ones used in fluid dynamics. During the last years, efficient multi-scale methods (of moments) were developed and present a great potential of application for meteorological purpose, what makes their further development and their validation relevant for modelling of population dynamics and application to hydrometors and therefore justify the purpose of this multi-disciplinary project.
The relevant microscale processes of cloud physics can be described by a (spectral) balance equation for the size distribution function f(x,t,r) of the different types of hydrometeors (or so called Population Balance Equation or PBE, see [1]). In case of spherical particles, the equation can be written:
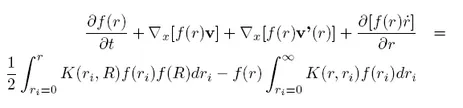
where the coordinates for position x=(x,y,z) and time t where not written in f and v for clarity purpose. This so-called spectral kinetic equation describes the temporal evolution of the particle population taking the effects of resp. convective and diffusive transports (with velocity resp. v and v'), condensation or evaporation (term with time derivative of r) as well as coagulation (right-hand side) into consideration, wherein R=(r3-ri3){1/3} is the radius of a partner particle so that two particles with radius resp. ri and R merge to form a particle with radius r. Nucleation and break-up processes are not considered in this equation. Moreover, other hydrometeors (ice particles, snow, hail) can also be described by such equations.
In principle it is possible to discretize this PBE in time and space coordinates, as well as in the so-called internal coordinate r and to solve it numerically (so-called spectral method). However the computational costs for this approach are extremely high, what makes it really difficult to affoard. A promising method, so-called method of moments (MoM),consists in considering some moments of the particle size distribution:

By integrating the PBE over the internal coordinate, evolution and transport equations for the moments can be derived, which will provide a description of the population dynamics. In the case of pure sedimentation in a 1D space (particles falling down without any condensation/evaporation, nucleation, coagulation/break-up processes) one can write the moment transport equation
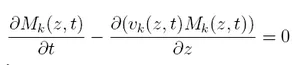
wherein vk = &intrkVF(z,r)f(z,t,r)dr/Mk is the moment velocity (for Mk) and VF the terminal velocity of the particle. A physical interpretation can be made for each moment (e.g. M3 is proportional to the volume fraction of the particles), what allows one to use experimental data for simulations. Nevertheless, the formulation of these moment transport equations often leads to the need to know a moment of higher order to solve the transport equation for a moment of a given order : it is the so-called closure problem. In order to resolve this problem, several approaches are available. One can assume which form the particle size distribution has (e.g. Normal, Gamma, Beta, ...) and find its parameters in order to reconstruct the moments of higher order : this is the presumed function MoM (pMOM or pNDFMOM, see [2]). An other approach consists in using the Gauss quadrature to estimate the integral terms thanks to weighted sums of evaluations of the integrand at special points (called abscissae) : in this method called quadrature MOM (or qMOM), no form is assumed for the particle size distribution (see [3]). Finally, an other method (called direct quadrature MoM or DQMOM, see [4]) newly derived from the qMOM has already been considered and the results obtained until now were promising as they were accurately capting complex processes such as growth, break-up and transport processes for multi-phase flows with disperse phases.
Goals
Several more or less complex methods of moments shall be investigated and developed, so that realistic collision and break-up kernel functions, which cannot be described with polynomials, as well as nonlinear drop growth rate functions, can be considered. Moreover, known structural defects and inherent uncertainties of the methods used previously shall be investigated and corrected. In particular, it should be investigated whether the unrealistic shock waves occurring in solutions for sedimentation cases computed thanks to usual methods of moments can be avoided with the help of these new methods of moments. Validations of these methods shall be carried out on the basis of zero and one dimensional models from cloud physics, in which the detailed spectral kinetic equation for the size distribution of the hydrometeors is numerically solved, as well as on the basis of experimental results.
References
[1] Pruppacher, H. R., and Klett, J. D. : Microphysics of Clouds and Precipitation. Kluwer Academic Publisher, 1997.
[2] Seifert, A., and Beheng, K. : A Two-moment Cloud Microphysics Parameterization for Mixed-phase Clouds. Part 1 : Model Description. Meteorologic and Atmospheric Physics 92 (2006), 45–66.
[3] McGraw, R. Description of aerosol dynamics by the quadrature method of moments. Aerosol science and Technology 27 (1997), 255–265.
[4] Marchisio, D. L., and Fox, R. O. Solution of population balance equations using the direct quadrature method of moments. Journal of Aerosol Science 36, 1 (2005), 43–73.