Computational Thermo-Fluid Dynamics
| Credits | 4 SWS, 4 ECTS |
| Contact | Varrilon, Grégoire |
| Sessions | Thursday, lecture 9:30-11:30 a.m. and hands-on 13:30-17:00 p.m. (9 sessions) |
| Rooms | MW 1701 (lecture) and MW 0704 (hands-on) |
The Associate Professorship of Thermo-Fluid-Dynamics cooperates with the Center of Key Competencies (Zentrum für Schlüsselkompetenzen) and offers teamwork and presentation workshops, which are undertaken during this lab course. The aim of this workshops is to combine the technical with the soft skill training.
The date for the team workshop and presentation workshop will be announced in one of the first lectures.
| Type | practical training |
|---|---|
| Term | Sommersemester 2024 |
| Language of instruction | English |
Admission information

Write your own numerical solver
- and therefore -
Understand by doing the general structure of a typical CFD solver
Build your own mesh
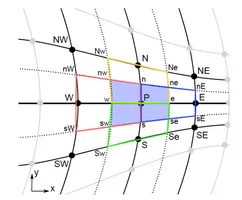
Discretize Equations

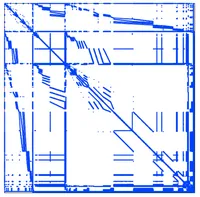
Solve system of Equations
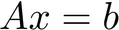
Understand numerical schemes
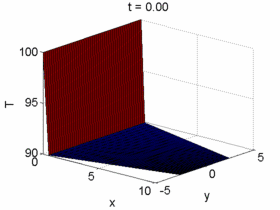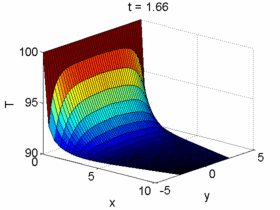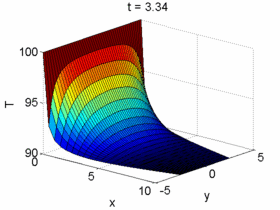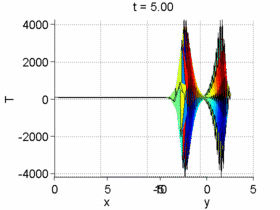
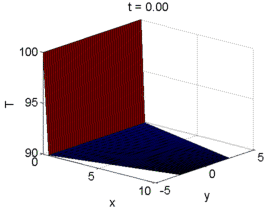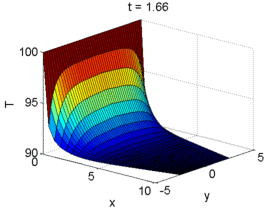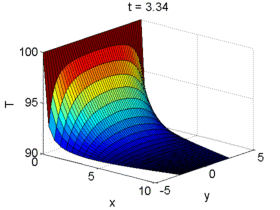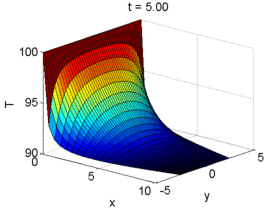
Post-treat Solutions
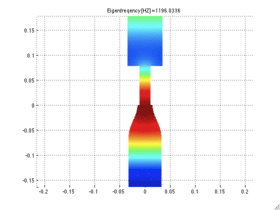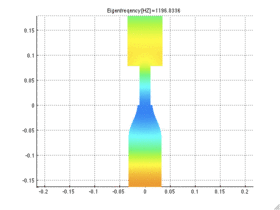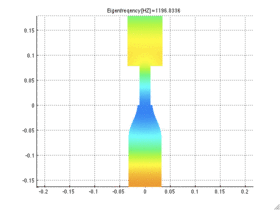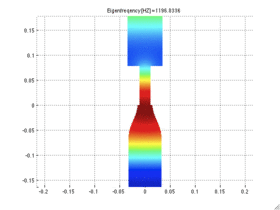
Objectives
Upon completion of the module, students are able to:
1) Recognize the classical operators (Gradient, Laplacian, etc) of convection-diffusion-reaction (CDR) equations in the context of Thermo-Fluid dynamics, as for example the Navier-Stokes Equations and the Energy equation.
2) Understand the structure of a given linear CDR equation (hyperbolic, parabolic, elliptic) and, accordingly, choose an appropriate numerical discretization for such an equation.
3) Implement in matlab, in an efficient way, fundamental numerical methods used in thermo-fluid dynamics to solve not only the heat equation (diffusion equation) but also other linear and non-linear CDR equations. In all sessions two dimensions are considered in structure-grids that may be non-Cartesian, so that complex geometries can be also taken into account.
4) Since the implementation is 100% done by the students with no external source code, the students will be able to understand in depth, by doing, the general structure of a typical Computational Fluid Dynamic (CFD) solver. The students are capable of building own meshes, discretizing the equations, solving the corresponding system of equations and post-treating the solutions. This is done by means of their own written numerical solver.
5) Perform analytical and numerical approaches to evaluate convergence and stability of the numerical approach implemented.
6) Implement classical iterative techniques to solve linear systems characterized by sparse matrices.
7) Understand, derive and implement techniques to solve linear PDEs that are based on integral equations (Green functions).
1) Recognize the classical operators (Gradient, Laplacian, etc) of convection-diffusion-reaction (CDR) equations in the context of Thermo-Fluid dynamics, as for example the Navier-Stokes Equations and the Energy equation.
2) Understand the structure of a given linear CDR equation (hyperbolic, parabolic, elliptic) and, accordingly, choose an appropriate numerical discretization for such an equation.
3) Implement in matlab, in an efficient way, fundamental numerical methods used in thermo-fluid dynamics to solve not only the heat equation (diffusion equation) but also other linear and non-linear CDR equations. In all sessions two dimensions are considered in structure-grids that may be non-Cartesian, so that complex geometries can be also taken into account.
4) Since the implementation is 100% done by the students with no external source code, the students will be able to understand in depth, by doing, the general structure of a typical Computational Fluid Dynamic (CFD) solver. The students are capable of building own meshes, discretizing the equations, solving the corresponding system of equations and post-treating the solutions. This is done by means of their own written numerical solver.
5) Perform analytical and numerical approaches to evaluate convergence and stability of the numerical approach implemented.
6) Implement classical iterative techniques to solve linear systems characterized by sparse matrices.
7) Understand, derive and implement techniques to solve linear PDEs that are based on integral equations (Green functions).
Prerequisites
Mathematics (analysis, Divergence and Green’s theorem, Ordinary differential equations)
Thermodynamics and heat transfer (Energy equation. Concept of energy, temperature, heat conductivity, conjugate heat transfer)
Basic Matlab
Thermodynamics and heat transfer (Energy equation. Concept of energy, temperature, heat conductivity, conjugate heat transfer)
Basic Matlab
Teaching and learning methods
The concepts and methods are introduced in a one-hour lecture. Subsequently, groups of two are formed to work in matlab during the practical session, which last around 5 hours. Two assistants are fully available during this time to guide the students to the completion of the practical exercises proposed.
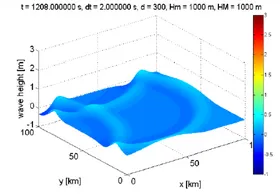
One very important part of the course is the final project. This project consists in writing a code to solve a set of CDR equations or a given wave equation of interest (Incompressible Navier-Stokes equations, Shallow-water equations, Potential flow equations, Stream-vorticity function equations, Helmholtz equation, etc). The projects proposed are based on realistic problems. In order to validate results, experimental or CFD data may be available. All projects consider two (or more) dimensions in structured grids that may be non Cartesian.
One very important part of the course is the final project. This project consists in writing a code to solve a set of CDR equations or a given wave equation of interest (Incompressible Navier-Stokes equations, Shallow-water equations, Potential flow equations, Stream-vorticity function equations, Helmholtz equation, etc). The projects proposed are based on realistic problems. In order to validate results, experimental or CFD data may be available. All projects consider two (or more) dimensions in structured grids that may be non Cartesian.
Examination
The software routines developed by the students will be evaluated according to functionality, structure, precision and robustness. Clear documentation – through commented code and supplementary material – is also important. The quality of the report on the term project and presentation influence also the evaluation.
Links
Examples of Final Projects (using students own solvers)
Incompressible Navier-Stokes Equations
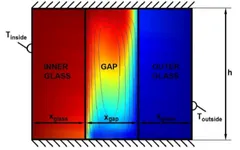
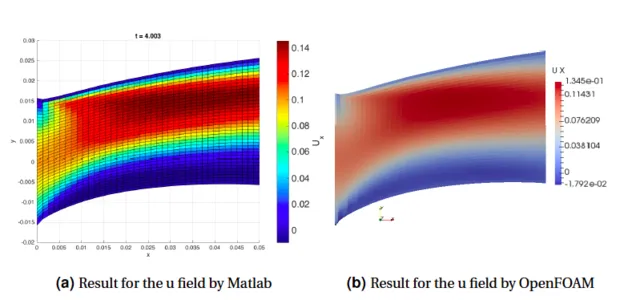
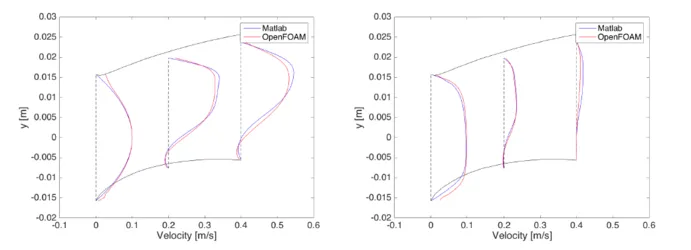
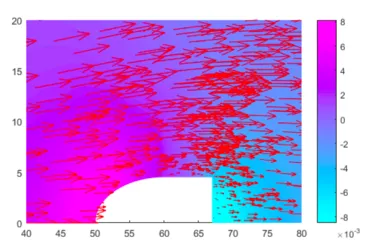
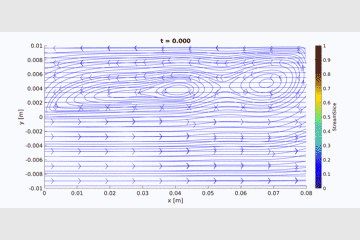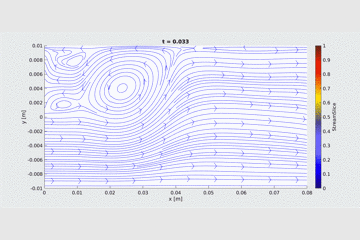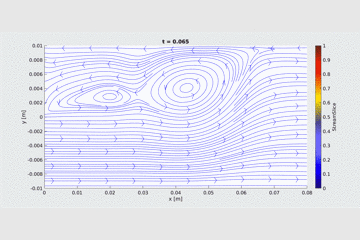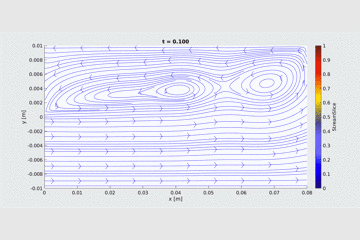
Stream-Vorticity Equations
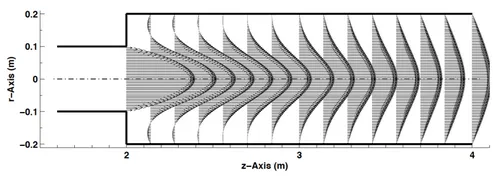
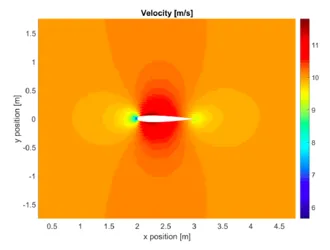
Potential flow
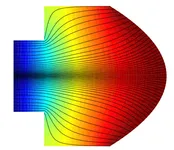
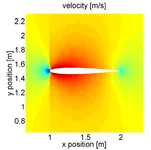
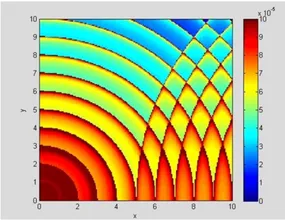
Green Functions and Wave Equation
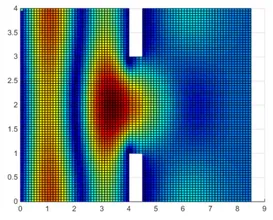
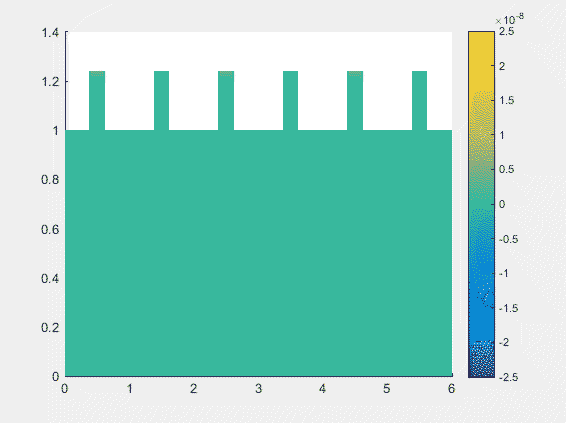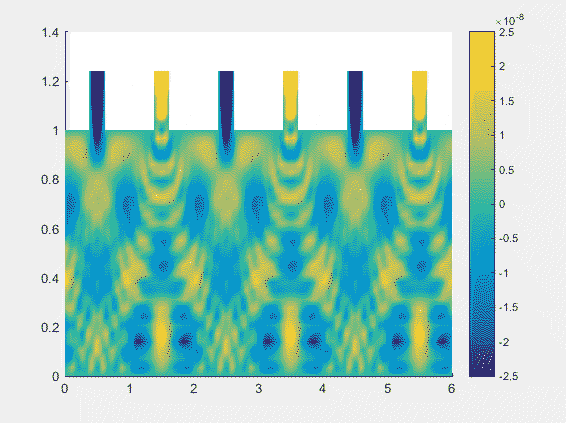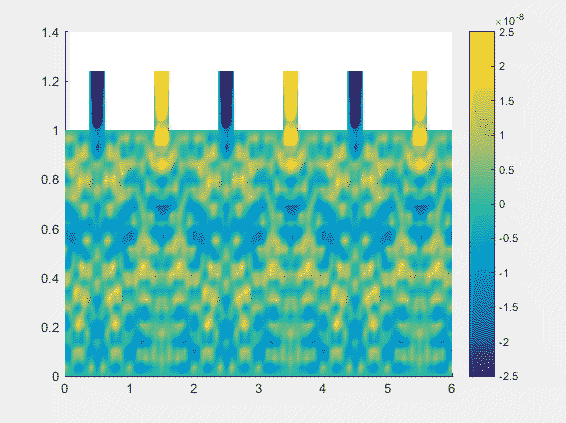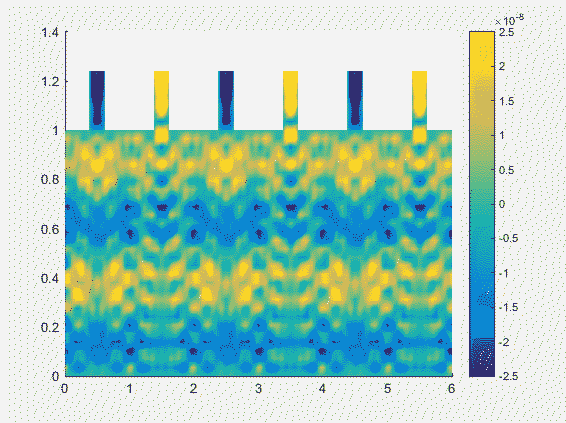
Shallow-Water Equations