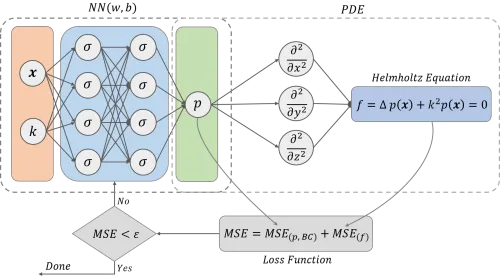
Conventional simulation models in computational vibroacoustics are often based on the finite element method (FEM) or the boundary element method (BEM). These require high computational times in industrial applications leading to delays in the design process. In addition, computationally expensive models are inefficient in terms of uncertainty quantification, which is essential for robust design decisions.
Data-driven deep learning (DL) methods intend to circumvent these problems and the idea is to develop efficient data-driven surrogate models that enable fast and accurate predictions including the model uncertainties for robust decision making. Since the amount of training data in computational vibroacoustics is usually limited, we particularly focus on research in the area of data-efficient methods like "physics-informed deep learning", where the underlying physical laws (e.g. the Helmholtz equation) are implemented as constraints in the loss function of the neural networks. This allows predicting meaningful results in the presence of small training data and the inherently stochastic methods allow an immediate uncertainty quantification.