Since the 1950s, aeroacoustics as a special research field in acoustics has gained much attention. Industrial applications such as the noise reduction in aircraft cabins, analyzing the dynamic loading of spacecraft payloads or the noise emission of HVAC-systems in automotive applications have led to an increase in research activities.
Based on fundamental continuum mechanics, a number of reformulations of the Navier-Stokes equations are known. These include the Linearized Euler Equations (LEE), the Linearized Navier-Stokes Equations (LNSE), the Acoustic Perturbation Equations (APE) and Galbrun’s equation which can be used to analyze acoustic wave propagation in moving media. At the Chair of Vibroacoustics of Vehicles and Machines, research is conducted towards analyzing aeroacoustic phenomena described by Galbrun’s equation which is based on utilizing a mixed Lagrangian-Eulerian frame. The resulting unknowns are only the particle displacements of the fluid instead of the fluid’s density, velocity and pressure. We are applying the finite element method to discretize complicated acoustic domains and apply various boundary conditions to study physical phenomena of acoustic wave propagation. Our research goal is to identify modal contributions of acoustic domains subjected to background fluid motion. Since numerical difficulties arise when utilizing standard Galerkin methods, discontinuous Galerkin (DG-FEM) approaches are applied which show significant improvements towards numerical stability.
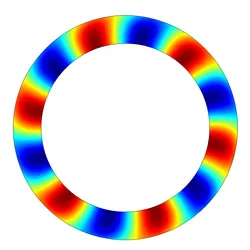
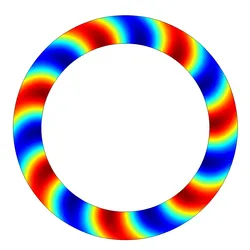
Typical example are the swirling flow of an aircraft turbo engine or the flow in a radial fan. In first approximation, both can be regarded as two dimensional problems. Since the flow introduces an asymmetry to symmetric circular problems, double modes split up and become complex in the mathematical sense. This complexity results in a co-rotating and a counter-rotating mode with respect to the circular flow motion.
Understanding these complex modes and there stability is crucial when understanding the acoustic wave propagation within flow regimes.