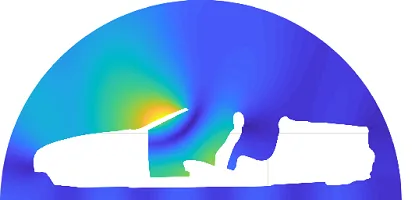
The analysis of sound propagation in closed domains is clearly limited in space by prescribed boundaries, e.g. the walls in case of room acoustics. But how does one model the influence of an open window or the sound radiation of a vibrating structure into an exterior domain of infinite extent, such as the cabriolet model in Fig. 1. Such problems are denoted as acoustic exterior domain problems. The solution of an exterior domain problem has to fulfill an additional boundary condition besides the conventional boundary conditions – the Sommerfeld radiation condition. This specific boundary condition demands the sound pressure amplitude to decay to zero with increasing distance from the sound source. Common methods to treat such exterior domain problems are the boundary element method or the finite element method under consideration of absorbing elements, perfectly matched layers as well as the infinite element method.
Intense research at the Chair of Vibroacoustics of Vehicles and Machines deals with the boundary element method and the application of infinite elements for vibroacoustic exterior domain problems. The specific formulation of the infinite elements enables the calculation of acoustic exterior modes – also called normal modes. These modes offer the possibility to solve exterior domain problems by use of the modal superposition technique or to project complex models down to a modal subspace. The identification of significant modes and their corresponding resonance frequencies enable the reliable prediction of noise reduction properties of novel sound absorption systems, such as acoustic metamaterials or sonic crystal sound barriers.
Current research at the institute deals amongst others with the determination of exterior modes of strongly-coupled systems accounting for fluid-structure-interaction, as for example for submerged thin-walled structures. Furthermore, the analysis of the transfer behavior of the system in modal coordinates is of research interest. The transfer behavior gives information for an efficient choice of modes for sound pressure field reconstruction and model reduction.