Geometric Modeling and Control of Flexible Robots

Modern robotic systems can solve highly complex problems with remarkable efficiency, which is often enabled by increasingly complex and partially flexible mechanical structures.

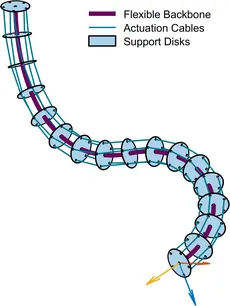
An important example of robots with highly flexible elements are soft robots and continuum manipulators. So-called cable-driven continuum manipulators consist of a highly flexible backbone, which can continuously deform along its entire length and take on complex shapes, and cables (or tendons) routed along the backbone, which are actuated at the base. These robots have (among others) important applications in medical engineering (e.g., for minimally invasive surgery and steerable catheters), in inspection tasks, or manufacturing.

This project focuses on developing structured, numerically efficient methods for modeling, simulation, and model-based control of rigid-flexible robotic systems, such as continuum manipulators.

Geometric modeling of flexible multibody systems

In our modeling approach for multibody systems – i.e., systems of rigid bodies connected with joints or flexible elements --, we aim to preserve and exploit the mathematical structures inherent to such systems. The kinematics of rigid bodies moving in 3D space, consisting of translation and rotation, is naturally described by a Lie group -- the special Euclidean group. This structure can be used to intrinsically consider the complex interaction of rotation and translation elegantly and compactly, resulting in an efficient modeling approach that is physically meaningful, highly structured, and easy to implement in simulation and control tasks.

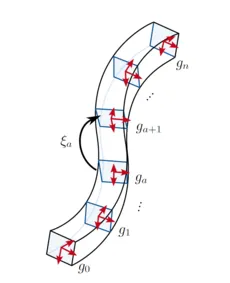
Highly flexible components are modeled as geometrically exact beams – a general, powerful approach that allows to accurately describe the statics and dynamics of flexible structures undergoing even large deformations. Remarkably, these models have a similar mathematical structure to rigid multibody systems since the configuration of a geometrically exact beam is described by a series of cross-sections along a center line, each behaving like individual rigid bodies in space.

We preserve this Lie group structure under spatial discretization, which is necessary to obtain finite-dimensional models usable for simulation and controller design from the continuous, infinite-dimensional beam models. Preserving the Lie group structure results in high accuracy, even at coarse discretization levels. In the discretized beam, we use relative variables to describe its configuration, which not only results in an efficient minimal model but also simplifies the integration into combined rigid-flexible multibody systems. Very importantly, it also allows us to precisely select which deformation modes (bending, torsion, shear, elongation) should be included in the model in a straightforward way and without using algebraic constraints. This is crucial to achieving good numerical performance since including stiff deformation modes (such as elongation or shear) would require very fine time steps and, thus, high computational effort.

Overall, we work on well-structured, efficient, and general models for tree-structured rigid-flexible multibody systems. The resulting models are implemented in a MATLAB toolbox that will be made publicly available in the future.

Time integration using (Lie group) variational integrators

For accurate yet computationally efficient time integration, we work in the framework of (Lie group) variational integrators. These implicit integrators are based on discrete-time analogs of continuous-time mechanical principles – such as Hamilton’s principle – and result in intrinsically discrete equations of motion, which can preserve the underlying Lie group structure and important physical quantities such as momentum. Moreover, they are symplectic by construction, which gives them excellent long-term energy behavior. Due to this preservation of mathematical and physical structures, variational integrators can achieve accurate results even at large time steps, giving them high numerical efficiency as required in the context of real-time applications.

Model-based (optimal) control of continuum manipulators

One of the primary applications of the developed system models is optimal control, where we aim at efficient and accurate methods that can reliably solve practically relevant problems. Consistent with our discrete-time modeling approach, we solve optimal control problems (OCPs) in the framework of discrete mechanics and optimal control (DMOC), where we discretize the continuous-time control problems using the discrete variational methods outlined above. This directly results in nonlinear programming problems (NLPs) that are easy to implement, computationally efficient, and numerically robust.

Additionally, we investigate observer-based controller structures, e.g., for position or force control of rigid or flexible robot manipulators.