Uncertainty Quantification in Computational Fluid Dynamics for the assessment of combustion instabilities
by Camilo Silva and Wolfgang Polifke
Motivation
For a robust design of systems, Uncertainty Quantification (UQ) studies must be carried out in order to evaluate the performance and safety of the system of interest under off-design operating conditions (small or large deviations from the desired operating point). In later years, Computational Fluid Dynamics (CFD) has gained notable recognition for the conception of systems at defined operating conditions. Nevertheless, since CFD (RANS, LES, DNS) is a numerical approach generally characterized by expensive computations, UQ studies, which are commonly based on results collected through numerous realizations (of the order of tens of thousands), are prohibitive. Nowadays, as a result, most of UQ numerical studies do not consider CFD but, instead, consider robust surrogate models of the system of interest.
Adjoint Helmholtz Solver
Helmholtz solvers have been of great utility for the study of thermoacoustic instabilities in academic and industrial combustion chambers. They rely on the efficient solution of the homogeneous Helmholtz equation by algorithms devoted to large Eigenvalue problems. Nevertheless, these type of solvers are still computationally expensive if Monte Carlo simulations are required for UQ studies. Consequently, a surrogate model is required that is computationally affordable and that deliver reliable results. In this study, this is done by a so-called Adjoint Helmholtz solver. The nonlinear eigenvalue problem and its adjoint are solved by an in-house adjoint Helmholtz solver, based on an axisymmetric finite volume discretization. In addition to first-order correction terms of the adjoint formulation, as they are often used in the literature, second-order terms are also taken into account. Finally, the probability density function (PDF) of the growth rate in the presence of uncertainties in the input parameters is calculated with a Monte Carlo approach. The uncertainties considered concern the gain and phase of the flame response, the outlet acoustic reflection coefficient, and the plenum geometry.
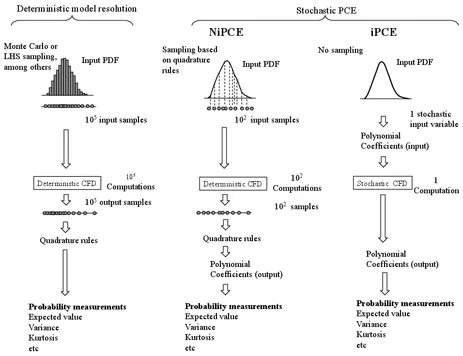
Polynomial Chaos Expansion
Most of the time, two steps are most of the time followed in order to carry out UQ based on CFD simulations:
- Simplification of the equations: CFD simulations are computationally expensive since two or more strongly coupled non-linear equations must be solved for (generally) millions degrees of freedom. In order to decrease the computational cost, surrogate models are derived from the CFD equations around a given operating condition. As a result, their solution becomes computationally affordable (from hours to some minutes).
- Solve several times the system of Equations: In order to collect sufficient statistical data, multiple computations must be performed on the surrogate model. In order to avoid Monte Carlo simulations, “smart” sampling techniques are sometimes preferred as Latin Hypercube method, Lattice-based sampling, among others [1-3]. Quadrature methods are subsequently applied in order to compute the stochastic measures of interest.
The UQ procedure based on surrogate models, as the adjoint method described in the previous section, has several limitations. On the one hand, only small uncertainties of the inputs around the design point can be accounted for, because the equations are valid only for a certain (fix) operating condition. On the other hand, a considerable amount (of the order of tens of thousands) of realizations must be computed, in order to have sufficient statistical information to quantify the output statistical properties of interest (mean, variance, skewness, etc) of the output quantity under investigation. The PCE project will be essentially devoted to the study of novel methodologies for the application of UQ in CFD based on Polynomial Chaos Expansion (PCE), a technique that has gained attention only since very recently. This approach has enormous potential because, if correctly understood and applied, uncertainties of the outputs can be quantified by solving only once the set of equations that characterize the system. In order to do so, the set of equations should be modified by replacing deterministic variables to the stochastic counterparts. Since recent years, PCE techniques have received considerable attention mainly from the mathematic community [2-4]. A big amount of knowledge has been collected for fundamental 1D/2D cases such as the heat equation, incompressible Navier-Stokes (laminar) equations, Burgers equation. In addition, significance importance has been given to the stochastic model of turbulence through PCE. During those studies, some potentials as well as some limitations of PCE methods have been recognized. For example, today it is known that both a large degree in the polynomial expansion and a large amount of independent input random variables may lead to the so-called “curse of dimensionality”. In despite of this advances, little attention has been given to more complex cases (turbulent non-reactive/reactive flows) where the turbulence is modeled as a deterministic variable (as RANS or LES), and where the uncertainties come fundamentally from the boundary conditions. The later will be the main concern of this project. The present study will profit of the mathematical background developed in the field of PCE to bring the method to a new level. The work is organized in three interconnected topics: UQ studies on non-reactive incompressible turbulent systems; UQ studies on linearized thermo-acoustic fields; and UQ studies on laminar flames.