Multi-Scale Analysis of Thermoacoustic Combustion Instability
Motivation and Background
Thermoacoustic combustion instability comprises processes evolving at a variety of length and time scales. The ratios of hydrodynamic length scale and acoustic wavelength, and of convective velocity and the speed of sound are described by the Helmholtz (He) and Mach (Ma) number, respectively. In typical applications, such as acoustically compact flames in subsonic flow, both He and Ma become very small. Consequently the discrepancy between length scales and velocities is large, whereas the time scales coincide. On the one hand, this coincidence of time scales implies a close coupling of acoustics to hydrodynamics and combustion, such that the different sub-problems cannot be solved independently. On the other hand, the discrepancy of length and velocity scales makes the numerical solution of the coupled problems very expensive, as all scales must be resolved.
A common approach to solve thermoacoustic problems is the coupling of a model for the propagation of acoustic waves with a suitable flame model. The acoustic model is derived from linearized Euler equations, relying heavily on many ad-hoc assumptions, such as vanishing viscosity and infinitely small amplitudes of acoustic waves. The only source term for acoustics present, that accounts for the interaction with hydrodynamics and combustion, is the fluctuating heat release in the energy equation. This source term is described by the flame model, that is usually identified from data of the hydrodynamic system (or the fully compressible system), where viscous effects and nonlinearities are present again. Thus, the two models employ different, conflicting assumptions regarding viscous effects and (non-)linearity. Furthermore, the structure of the flame model and its input and output channels are also prescribed and subject to ad-hoc assumptions.
In the present project, sub-models for acoustic and hydrodynamic phenomena are derived in a mathematically sound manner. Starting from equations involving as few assumptions as possible, i.e. compressible reacting Navier-Stokes equations, a multi-scale asymptotic expansion is carried out. The results are different sets of equations describing processes evolving at the different length scales and the appropriate coupling terms.
Asymptotic Analysis
The compressible Navier-Stokes equations are a prime example of a singular perturbation problem. That is a small or large parameter premultiplying the highest derivative of some variable. In the limit where this highest derivative vanishes, the equation changes qualitatively, e.g. from parabolic to hyperbolic. Such behavior is usually linked to the existence of different scales as, for instance, boundary layers in otherwise inviscid flow. In the case of the Navier-Stokes equations it is the prefactor 1/Ma² of the pressure gradient that causes the disparity of scales for small Mach numbers. In asymptotic analysis the variables are expanded in a series of terms of increasing order in Ma:
Φ = Ma0 Φ0 + Ma1 Φ1 + Ma2 Φ2 + …,
thereby yielding a leading order solution and subsequent higher order corrections. Furthermore, to separate effects evolving at different scales, the derivative operators must be expanded, too:
∇ = ∇x + Ma ∇ξ,
where x and ξ denote spatial coordinates scaled with the hydrodynamic and acoustic length scale, respectively.
Gathering terms of equal order in Ma, and elimination of mixed derivatives in spatial scales by appropriate filtering operators finally separates short and long length scale phenomena and uncovers the coupling relations between them.
Advanced Model Structures
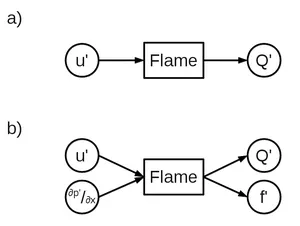
The application of multi-scale asymptotic analysis to compressible reacting flows allows to identify the interactions between hydrodynamics/combustion and acoustics. In Figure 1, the model structure derived from asymptotic analysis is compared to the model structure that is commonly used to date. Unlike in common flame models, the hydrodynamic fields not only react to acoustic velocity perturbations u' at the inlet, but also to a so-called global acceleration term. This term corresponds to the acoustic pressure gradient ∂p'/∂x. A suitable flame model should thus require two input channels, and it is very likely that the response of the flame is depending on the impedance or position of the flame relative to the surrounding acoustic field. Moreover, a second driving mechanism of acoustics is identified: In addition to the fluctuating heat release Q', that affects the acoustic energy, the dilatation of the flow field acts as a source of acoustic momentum f'. Consequently, the model structure derived from asymptotic analysis comprises two output channels as well.
Project Outline
The equations derived from asymptotic analysis are implemented in the open source software OpenFOAM®. In order to decrease computational demand, an embedded domain approach is used, as depicted in Figure 2. While acoustic waves propagate through the entire domain, effects of hydrodynamics and combustion are confined to a small area around the position of the flame. Thus, a fine computational mesh needs to be employed only in this sub-domain. The coarse mesh, resolving large scale acoustic waves only, covers the entire domain, overlapping the hydrodynamic sub-domain. Appropriate anti-aliasing filters and interpolation operators allow to map the coupling terms from one mesh to the other. The embedded domain model is validated against a brute force solution obtained from a fully compressible Navier-Stokes code. In particular flame transfer function and scattering behavior of acoustic waves is compared. The influence of the different coupling terms is assessed to draw further conclusions on the structure of reduced order, input-output models obtained by means of system identification.
Acknowledgements
The present work is the continuation of DFG project PO 710/12-1, and of work financially supported by the Technische Universität München – Institute for Advanced Study, funded by the German Excellence Initiative.