PAML - Physics Augmented Machine Learning for Thermoacoustic Modeling

The transition towards hydrogen-based combustion in gas turbines and aircraft engines is crucial in our fight against climate change. These advanced systems offer a promising path to reducing greenhouse gas emissions, but their development is challenging. A significant obstacle is the occurrence of thermoacoustic instabilities. These instabilities arise from the interaction of a flame with the system’s acoustics, resulting in high-pressure waves that can damage or even destroy the gas turbine/aircraft engine.
Traditionally, addressing these complexities has relied heavily on computational fluid dynamics (CFD) simulations. While comprehensive and accurate, CFD simulations demand extensive computational resources and time, making them bottlenecks in rapid testing and development cycles.

In recent years, the field of machine learning (ML) has seen widespread adoption across various engineering disciplines, emerging as a powerful tool for leveraging (existing) data to predict thermoacoustic behavior more effectively. However, the application of ML in thermoacoustics is challenged primarily due to the sparse and noisy nature of the available data. This situation raises concerns about the reliability and accuracy of ML-based predictions, both are particularly significant in thermoacoustics. In this field, achieving high prediction accuracy is crucial for ensuring the safety and efficiency of hydrogen engines.

To address these challenges, we intend to incorporate prior physical knowledge into the ML framework. The core of our methodology involves three strategic elements:

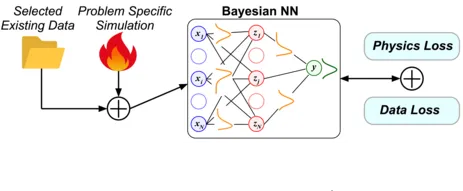
1. We analyze which data are most informative for understanding thermoacoustic behavior, ensuring that the ML models are trained on the most relevant datasets. Furthermore, we analyze if data from related problems helps reduce the required data for a good prediction.
2. We focus on the design of the ML model itself. We investigate several architectures/methods and analyze their performance concerning accuracy, reliability, and interpretability. Among these promising methods are Bayesian Neural Networks, which can incorporate physical priors into the model parameters and naturally model the uncertainty in the model weights and the resulting model predictions.
3. We explore the application of physical loss functions. In these loss functions, physical equations/constraints can be directly embedded into the model training, offering a robust mechanism to ensure that the model predictions fulfill the underlying physical problems. Furthermore, the physical loss could reduce the data required to train the model.