The OLG-LES Approach for the Determination of Thermoacoustic Stability

Thermoacoustic instabilities in technical combustion present a severe problem in a wide area of applications - rockets and gas turbines are affected as well as domestic combustion systems.

In order to prevent a costly redesign of instability prone systems, it is desirable to determine the acoustic stability behaviour in early design stages by numerical tools. One such method is the network model approach, which determines the properties of a system by dividing it into elements characterised by their transfer functions. These can be assembled to a system of equations and solved for eigenfrequencies. Another commonly used method is to simulate the entire domain with detailed CFD. If turbulence effects are relevant, which is often the case, and LES is employed, this model requires massive computing power.

These two conventional methods rely thus either on the knowledge of the transfer functions of all elements involved in the system, which cannot always be derived in a straight forward manner, or on heavy computational power in the case of CFD.

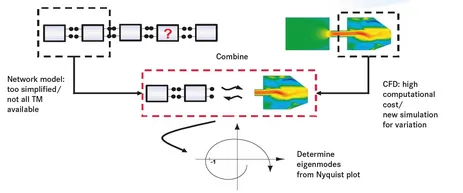
The hybrid OLG-LES approach developed in the present project joins these two methods in order to combine the power of LES for complex elements with the advantages of the network model for simple elements (see figure 1), thereby avoiding the shortcomings mentioned above of either method, while profiting from their advantages. For example, as opposed to the network model approach, correct acoustic boundary conditions cannot be implemented in CFD in most cases.

The OLG is defined by

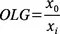
(see figure 2). It is thus a projection rule which projects all eigenmodes of the caracteristic equations to the so called critical point -1 in the complex plane. Plotting the OLG and using criteria similar to the Bode- and Nyquist-rules applied in control theory, the stability properties can be determined.

The OLG-LES method now simulates one part of a domain with high resolution CFD. This CFD-domain is excited with an acoustic signal xi and the response is recorded. This response is then processed by the network model representing the other parts of the system (see figure 1) resulting in the outgoing signal xo of the open control loop. Eigenmode analysis can then be performed by determining the OLG in a straight forward manner. The interface between the CFD and the network model provides a natural cut for the OLG.

Identifying the responding wave in the CFD part proves to be difficut in highly turbulent systems simulated by LES, as turbulence and noise can have the same order of frequency and amplitude.

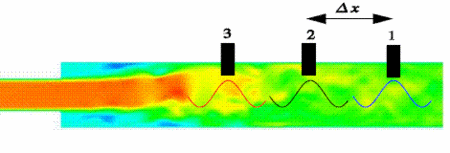
Using the fact that in contrast to turbulence, acoustic waves propagate with a characteristic velocity (the speed of sound), the two phenomena can be separated when pressure and velocity fluctuations are recorded at different locations of the system (see figure 3) by cancelling out turbulent fluctuations.

As a first validation case for the OLG-LES approach, a Rijke tube as one of the most simple thermoacoustic systems has been simulated. The Rijke tube has the advantage that an analytical solution is well known and the results from the OLG-LES method can thus be verified. Figure 4 shows that eigenmodes determined by the OLG-LES method coincide very well with the analytically determined values.