Deep Learning

Konventionelle Simulationsmodelle in der numerischen Vibroakustik basieren oft auf der Finite Elemente Methode (FEM) oder der Randelementemethode (BEM) und diese erfordern bei industriellen Anwendungen hohe Rechenzeiten, was den Entwicklungsprozess unnötig verzögert. Außerdem erschweren rechenintensive Modelle eine Quantifizierung der Modellunsicherheiten, was jedoch für eine robuste Entscheidungsfindung essentiell ist.

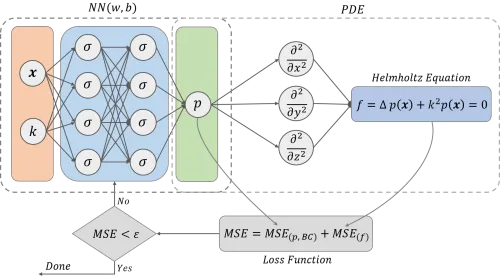
Der Einsatz von datengetriebenen Deep Learning (DL) Methoden soll genau diese Probleme umgehen und die Idee ist es, auf Basis von Daten effiziente Ersatzmodelle zu entwickeln, die schnelle und präzise Prognosen ermöglichen und aus denen durch die Kenntnis von Modellunsicherheiten robuste Konstruktionsentscheidungen abgeleitet werden können. Da die Datenbasis in der numerischen Vibroakustik üblicherweise begrenzt ist, erforschen wir speziell dateneffiziente Methoden des „physics-informed Deep Learnings“, wo die zugrundeliegende physikalische Gleichung (z.B. die Helmholtz-Gleichung) als Zwangsbedingung in die Verlustfunktion der neuronalen Netze implementiert wird. Dies erlaubt es, trotz geringer Trainingsdatenbasis aussagekräftige Ergebnisse vorherzusagen und die inhärent stochastischen Methoden ermöglichen unmittelbar eine Quantifizierung der Unsicherheiten.