Diskontinuierliche Galerkin-Verfahren in der Strömungsakustik
Seit den 1950er Jahren hat die Aeroakustik als Teilbereich der Akustik viel Aufmerksamkeit gewonnen. Insbesondere für industrielle Anwendungen wie die Lärmreduzierung in Flugzeugkabinen, die Analyse der dynamischen Belastung von Raumfahrzeugen oder die Geräuschemission von Klimaanalgen in der Automobilindustrie hat zu einer Zunahme der Forschungsaktivitäten geführt.
Basierend auf der fundamentalen Kontinuumsmechanik können eine Reihe von Neuformulierungen der Navier-Stokes-Gleichungen, bekannt als Linearized Euler Equations (LEE), der Linearized Navier-Stokes Equations (LNSE), der Acoustic Perturbation Equations (APE) oder der Galbrun-Gleichung zur Analyse der Ausbreitung akustischer Wellen in bewegten Medien verwendet werden. Am Lehrstuhl für Akustik mobiler Systeme wird an der Verwendung der Galbrun-Gleichung zur Analyse aeroakustischer Phänomene geforscht. Diese Formulierung basiert auf einer gemischten Lagrange-Euler‘schen Betrachtungsweise. Die daraus resultierenden Unbekannten sind nur die Fluidpartikelverschiebungen anstelle von Dichte, Geschwindigkeit und Druck des Fluids. Wir setzen die Finite-Elemente-Methode ein, um komplexe akustische Domänen zu diskretisieren und verschiedene Randbedingungen anzuwenden, damit die Effekte in Bezug auf die Ausbreitung akustischer Wellen untersucht werden können. Das Ziel ist es, modale Beiträge in akustischen Gebieten zu identifizieren, die einer Hintergrundströmung ausgesetzt sind. Da numerische Schwierigkeiten bei der Verwendung von Standard-Galerkin-Methoden auftreten, werden diskontinuierliche Galerkin (DG-FEM) Ansätze angewendet. Diese zeigen eine signifikante Verbesserungen im Bezug auf die numerischer Stabilität.
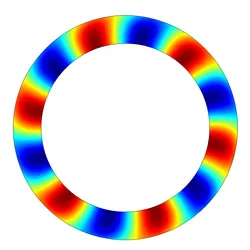
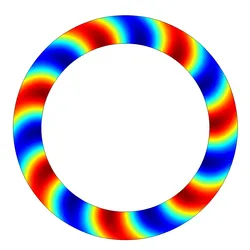
Typische Anwendungsbeispiele sind die Drallströmung eines Flugzeugtriebwerks oder die Strömung in einem Radialventilator, welche in erster Näherung als zweidimensionale Probleme angesehen werden können. Da die Strömung eine Asymmetrie zu symmetrischen Kreisproblemen einführt, werden Doppelmoden aufgeteilt und besitzen im mathematischen Sinne komplex Anteile. Diese Komplexität führt in Bezug auf die Kreisströmungsbewegung zu einer gleichsinnig und einer gegenläufig drehenden Mode.
Das Verständnis dieser komplexen Modi und ihrer Stabilität ist entscheidend für das Verständnis der akustischen Wellenausbreitung in Strömungssystemen.