Fluid-Struktur-Interaktion

Abb. 1: Energiedissipation durch Schallabstrahlung trägt bei Leichtbaustrukturen wie dieser Sandwichplatte entscheidend zur Gesamtdämpfung bei.

Abb. 2: Darstellung der numerischen Modellierung einer Sandwichplatte und dem umgebenden akustischen Medium. Das FE-Netz der Struktur ist mit dem akustischen BE-Netz auf der schallabstrahlenden Oberfläche gekoppelt.

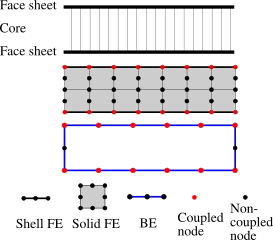
Die Lösung vibroakustischer Problemstellungen, wie sie beispielsweise in der Automobil- und der Luftfahrtindustrie auftreten, erfordert oftmals die Simulation von Struktur-Akustik-Interaktionen. Typischerweise erfolgt die Berechnung im Frequenzbereich und die elastodynamischen Gleichungen werden mittels der Finiten Elemente Methode (FEM) diskretisiert. Zur Modellierung des umliegenden, oftmals unendlich ausgedehnten akustischen Felds stehen verschiedene Methoden zur Auswahl. Am Lehrstuhl für Akustik mobiler Systeme beschäftigen wir uns dabei hauptsächtlich mit der Randelementemethode (BEM) und der Infiniten Finite Elemente Methode (IFEM). Des Weiteren sind wir besonders an Anwendungen interessiert, bei denen eine gegenseitige (starke) Kopplung zwischen der Strukturschwingung und der Fluidschwingung besteht. Dies ist vor Allem bei Leichtbaustrukturen aber auch bei Musikinstrumenten relevant. In diesen Fällen sind die Fluidlasten, die auf die Struktur wirken, nicht vernachlässigbar.

Aus numerischer Sicht erfordern vollständig gekoppelte Struktur-Akustik-Interaktionen einen großen Rechenaufwand – insbesondere bei stark variierendem Verhalten über einen großen Frequenzbereich. Um den Rechenaufwand zu verringern verwenden wir verschiedene Verfahren zur Model-Ordnungs-Reduktion (MOR). Dabei geht es vor Allem darum, einen Projektor zu bestimmen, der geeignet ist, die Dimension des vibroakustischen Problems zu reduzieren und somit Frequenzbereichslösungen zu beschleunigen. Der Projektor kann dabei entweder in einer Offline-Phase berechnet oder während der eigentlichen Simulation iterativ bestimmt werden.

Außerdem verwenden wir Modalanalysen als einen alternativen Ansatz zur Charakterisierung struktur-akustischer Systeme. Modalanalysen erfordern die Lösung eines oftmals nichtlinearen Eigenwertproblems. Als Ergebnis erhält man struktureigene Eigenschaften wie die nassen Eigenfrequenzen oder die modalen Werte für Dämpfung durch Schallabstrahlung. Letzteres quantifiziert das Ausmaß an Strukturdämpfung aufgrund von Schallabstrahlung ins akustische Fernfeld. Sobald die Moden einmal bestimmt sind, können die Strukturantworten bei verschiedenen Frequenzen und Anregungen durch einfache Matrix-Vektor-Multiplikationen errechnet werden.