Randelementemethode

Abb. 1: Konvergenz-Historie des Greedy-Verfahrens für ein akustisches Innenraumproblem. Es werden die relativen Residuen nach der 1., 6. und der 9. Iteration sowie das Residuum nach Konvergenz gezeigt. Nach der 6. Iteration sehen wir drei Maxima bei den Resonanzfrequenzen 100, 150 und 200Hz. Diese Frequenzen werden in den nachfolgenden Iterationen als Samplefrequenzen gewählt und führen damit zu einer schnellen Konvergenz.

Abb. 2: Schemaskizze der Grenzschichteffekte aufgrund thermischer und viskoser Verluste. Die Pfeile beschreiben die Schallschnelle im Ausbreitungsmedium. Die Farbcodierung gibt Auskunft über das Temperaturfeld im Fluid.

Die Randelementemethode (engl. Boundary Element Method, BEM) findet eine breite Anwendung zur Lösung einer Vielzahl technischer und wissenschaftlicher Problemstellungen aus der linearer Akustik. Dabei beschränkt sich die Modellierung auf den Rand des akustischen Mediums. Während die BEM besonders durch die implizite Erfüllung der Sommerfeld’schen Abstrahlbedingung besticht, liegt ihr größter Nachteil in der Frequenzabhängigkeit der Systemmatrizen und dem damit verbundenen numerischen Aufwand für Frequenzbereichslösungen.

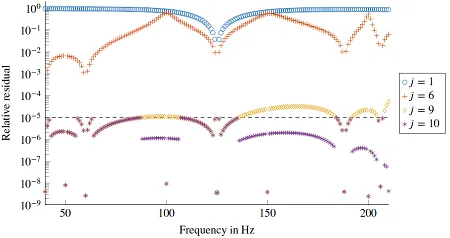
Daher sind wir am Lehrstuhl mit der Entwicklung effizienter Strategien für Frequenzbereichssimulationen beschäftigt. Einer unserer neueren Beiträge in diesem Zusammenhang ist das sogenannte Greedy-Verfahren. Da die Lösungen an vielen benachbarten Frequenzpunkten oftmals in einem kleinen Unterraum liegen, können sie mittels weniger Basisvektoren approximiert werden. Beim Greedy-Verfahren sind diese Basisvektoren die Lösungen an Frequenzpunkten, die iterativ mittels eines Optimalitätskriteriums ausgewählt werden.

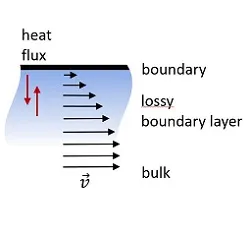
Weitere Forschungsvorhaben im Bereich der Randelementmethode beziehen sich auf die Implementierung thermoviskoser Verluste. Letztere werden bei der Modellierung von Schallwellen im akustischen Medium aufgrund ihres eher lokalen Charakters zumeist vernachlässigt. Bei einer Vielzahl von Anwendungen aus Industrie und Praxis spielen derartig kleinskalige Effekte jedoch eine entscheidende Rolle. Hierzu zählen vornehmlich Gerätschaften, wie bspw. Hörgeräte oder Mikrofone, deren Kavitäten die gleiche Größenordnung aufweisen wie die verlustbehaftete Grenzschicht. Unser Forschungsteam nutzt für die numerische Analyse die sog. Kirchhoff Decomposition. Dabei werden die linearisierten Navier-Stokes-Gleichungen in eine viskose, thermische und akustische Komponente aufgespalten, welche lediglich auf dem durch die BEM berechneten Rand der Domain interagieren. Die um die Verluste erweiterte Implementierung soll am Lehrstuhl für die Erforschung von Metamaterialien genutzt werden.